Сайт, посвященный ЕН-Антеннам. Статьи. Описания. Конструкции. Эксперименты. Результаты испытаний.

 

В статье рассматриваются принцип действия и параметры малогабаритной резонансной антенны (МРА) конденсаторного типа (С- антенны). Приводятся результаты расчета и измерения частотных зависимостей сопротивления и мощности излучения, а также экспериментальные диаграммы направленности С-антенны. Дана оценка сравнительной эффективности С-антенны и полноразмерной дипольной антенны.

 

МАЛОГАБАРИТНЫЕ РЕЗОНАНСНЫЕ АНТЕННЫ

Маслов О.Н., Рябушкин А.В., Шашенков В.Ф

ИНФОКОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ
Периодический научно-технический и информационно-аналитический журнал Том 8, №2, 2010
ISSN 2-37-3909
УДК 621.396.677; 621.397.671

(публикуется с разрешения редакции журнала и авторов, на сайте http://ehant.qrz.ru)

В статье рассматриваются принцип действия и параметры малогабаритной резонансной антенны (МРА) конденсаторного типа (С-антенны). Приводятся результаты расчета и измерения частотных зависимостей сопротивления и мощности излучения, а также экспериментальные диаграммы направленности С-антенны. Дана оценка сравнительной эффективности С-антенны и полноразмерной дипольной антенны.
Ключевые слова: малогабаритная резонансная антенна, конденсатор, ширина полосы частот, направленность, сопротивление излучения, мощность излучения.

Введение
В соответствии с первым уравнением Максвелла [1-2], наличие тока смещения

вляется одним из признаков системы, создающей электромагнитное излучение (ЭМИ), интенсивность которого характеризуется уровнем напряженности электрического поля Е в окружающей среде с абсолютной диэлектрической проницаемостью ε_a. Поскольку наиболее наглядным примером «концентратора» силовых линий тока смещения J_см служит конденсатор с сосредоточенной емкостью С, возбуждаемый с помощью длинной линии, рассмотрение принципа работы антенны часто начиналось со схемы, представленной на рис. 1а, где конденсатор показан

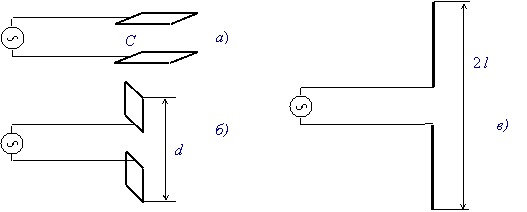
Рис. 1 Трансформация плоского конденсатора емкостью С в симметричную дипольную антенну [1 -2]

в обычном виде, с последующим переходом к схеме на рис. 16, где его обкладки развернуты на 180° (расстояние между внешними краями обкладок равно d) [1-2].
Увеличение излучающей способности системы при этом объясняли тем, что силовые линии вектора E в схеме на рис. 16 выходят далеко за пределы конденсатора, охватывая окружающее пространство. Следующим шагом был переход к системе с распределенной емкостью С (см. рис. 1в) между плечами симметричного вибратора, в которые трансформируются обкладки плоского конденсатора, то есть замена конденсатора дипольной антенной [1]. Первой реализацией излучателя такого рода является диполь Герца с емкостными нагрузками в виде шаров на концах плеч длиной l [2].

Традиционная теория и практика проектирования антенно-фидерных устройств (АФУ) однозначно подтверждают необходимость увеличивать электрические размеры антенны для повышения эффективности ее излучения. Поэтому диполь с размерами 2l/λ >> d/λ (см. рис. 16 и 1е), где λ - длина волны, при моделировании его излучающих свойств рассматривался также как разомкнутый и деформированный отрезок двухпроводной длинной линии (см. рис. 1в), обладающий резонансными свойствами [1-2]. В то же время остается открытым вопрос о том, во-первых, как будет резонировать и излучать система, показанная на рис. 16, если в ее состав ввести дополнительные реактивные элементы. И, во-вторых - можно ли на основе данной схемы реализовать МРА, а если можно - то какой излучающей способностью будет обладать такая антенна. Следует отметить, что интерес к резонансным системам ЭМИ на сосредоточенных элементах сегодня существенно возрос - в том числе благодаря обсуждению работ Н. Теслы, вокруг имени которого в этом отношении сложилось немало легенд.

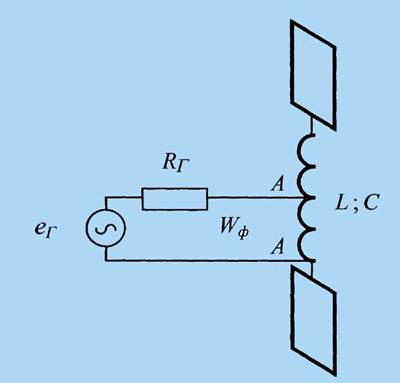
Рис. 2 Схема возбуждения С-антенны

Цель статьи - сравнительный анализ эффективности дипольной антенны и МРА конденсаторного типа (С-антенны), конструкцию и схему возбуждения которой в общем виде иллюстрирует рис. 2. Элементами МРА на рис. 2 являются развернутые обкладки конденсатора, емкость между которыми равна С, а также катушка индуктивности L с частичным подключением к ней в точках А-А фидерной линии с волновым сопротивлением W_ф, вход которой возбуждается генератором с ЭДС e_г и внутренним сопротивлением R_г.

Концепция и аналоги МРА

Рассматриваемые в статье С-антенны относятся к электрически малым АФУ - наряду с вибраторными антеннами с удлиняющими катушками индуктивности и магнитными резонансными антеннами, размеры которых не превышают 0,1 λ. По принципу действия к С-антенне близки ЕH-антенны [3-4] (название объясняется тем, что процессы формирования электрической Е-составляющей и магнитной H-составляющей ЭМИ в них разделены), а также SFRT-антенны [5] (антенны, реализующие технологию излучения синхронных полей - (Simultaneous Field Radiation Technology) и Crossed Field Antennas (CFA или антенны пересекающихся полей) [6]. Передающие CFA в настоящее время используются для радиовещания на средних волнах; более 20 видов ЕH-антенн для диапазона декаметровых волн выпускаются в США, Италии и Японии [4]. На перечисленные АФУ оформлены патенты, где сформулированы технические идеи и описаны основные варианты их конструкций. Например, [7] содержит концепцию ЕH-антенны, которая состоит в том, что ток и напряжение радиосигнала в ней должны быть сфазированы так, чтобы фазовый сдвиг между Е- и H-составляющими ЭМИ отсутствовал; рассматривается цилиндрическая ЕH-антенна и возможный принцип ее работы. В [8] аналогичным образом патентуются схема фазирования цилиндрической ЕH-антенны и варианты конструкции биконусной ЕH-антенны; предлагаются способы практического применения ЕH-антенн и т.п. Патент [9] защищает конструкцию CFA, предложенную специалистами из Великобритании и Египта.

Всегда считалось, что эффективность электрически малых АФУ не может быть высокой, поскольку сопротивление излучения R_Σ. у таких антенн, согласно [1-2], не превышает единиц Ом, что соизмеримо с сопротивлением активных потерь r. Поэтому КПД антенны η = R_Σ  /(r + R_Σ) здесь существенно меньше единицы, что является «платой» за малые габариты АФУ. Сказанное относится к антеннам всех типов, хотя для рамок известны конструкции, позволяющие получить приемлемый КПД - при обеспечении технологических норм на изготовление и применении высококачественных материалов для снижения r и достижения требуемой электрической прочности. В целом электрически малые АФУ широкого практического применения долгое время не находили.

В середине 1980-х лет в печати появились сообщения о строительстве электрически малых АФУ нового типа для СВ и ДВ радиовещания, скептически встреченные специалистами. Идеологом этих разработок был шотландский профессор Maurice Clifford Hately из Robert Gordon`s Institute of Technology, Aberden, UK (с 1992 г. - Robert Gordon University), который в 1988 г., совместно с аспирантом из Египта Fathi Mohammed Kabbary, впервые запатентовал CFA, эффективно излучающую при размерах в единицы процентов от λ. Впоследствии патенты на CFA были получены ими в США, Великобритании, Австралии, Японии, странах Евросоюза, Индии и Египте. Согласно [9], принцип работы CFA основан на раздельном формировании Е- и H-составляющих ЭМИ и создании уже в самом АФУ структуры ЭМИ, соответствующей дальней зоне излучения у традиционных антенн. Наиболее широкое применение CFA нашли на родине F.M. Kabbary в Египте, где он организовал фирму Kabbary Antenna Technology (KAT Company).

По данным Internet, после определенного кризиса, когда были разорваны контракты на строительство CFA на острове Мэн и в Китае, КАТ Company в сентябре 2009 г. построена и испытана (с привлечением независимой экспертизы) мощная CFA на частоту 1593 кГц высотой 8 м в городе Silsden, West Yorkshire, Великобритания, подтвердившая заявляемые характеристики. На сайте компании F.M. Kabbary приводит сравнительные результаты измерения уровней ЭМИ для CFA (с максимальными размерами 1-5% от λ) и традиционных антенн (вертикальные мачты и башни высотой λ/4), согласно которым CFA (для которой, к тому же, не требуется система противовесов или сложное заземление) в целом ряде случаев имела здесь преимущество.

В начале 1990-х годов к разработке электрически малых АФУ подключился американский инженер, радиолюбитель-коротковолновик Ted Hart, W5QJR - ранее известный как создатель малогабаритных рамочных приемо-передающих антенн. Основываясь на концепции Hately-Kabbery, T. Hart разработал собственные оригинальные конструкции, названные им ЕH-антеннами, более простые и удобные в реализации по сравнению с CFA [7-8].

Для некоммерческого использования ЕH-антенны T. Hart опубликовал в Internet программу расчета элементов ее конструкции и подробную инструкцию по настройке. Хотя основной рыночный спрос приходится на ЕH-антенны для радиолюбителей, через свою фирму T. Hart предлагает передающие АФУ на СВ и ДВ диапазоны. По данным [3] такая ЕH-антенна для АМ вещания с мощностью излучения до 10 кВт на частоте 700 кГц (с возможностью перестройки от 500 до 1200 кГц, общая длина менее 12 м), построенная в Эль Сальвадоре, Мексика, по уровню ЭМИ в дальней зоне не уступает стандартной антенне-башне, причем не нуждается в разветвленной системе заземления. Кроме АФУ на основе полых металлических цилиндров и конусов, T. Hart предложил вариант плоской ЕH-антенны.

Наиболее активными пользователями и пропагандистами электрически малых АФУ нового типа сегодня являются радиолюбители, опыт которых в основном подтверждает заявленные параметры данных антенн. В США интерес к SFRT-антеннам проявляют также компании, работающие в военно-технической сфере [5]. Опубликованные результаты экспериментов и опытной эксплуатации SFRT-антенн демонстрируют многообещающие свойства данных АФУ: малые размеры, повышенные широкополосность и внеполосная помехозащищенность, малочувствительность к посторонним внешним индустриальным и естественным Е- и H-полям и т.д.

В отечественном секторе Internet действуют сайты [10-11], где энтузиасты в области антенной техники делятся опытом изготовления и исследования эффективности применения разных вариантов реализации ЕH-антенн. Среди них выделяется В. Кононов (UА1АСО), который постоянно проводит эксперименты с ЕH-антеннами и публикует их результаты для обсуждения со всеми заинтересованными лицами. В то же время антенны данного типа пока не привлекли у нас внимание широкого круга научно-технических специалистов.

Принцип действия МРА

Принцип действия несимметричной МРА на примере CFA иллюстрирует рис. 3. По утверждениям авторов [3-9], им удалось конструктивно разделить процессы возбуждения Е-составляющей и H-составляющей высокочастотного ЭМИ и выровнять их по фазе в непосредственной близости от антенны (в самом АФУ), а не в дальней (волновой) зоне, как это имеет место, например, для диполя, показанного на рис. 1в. В конструкции CFA на рис. 3 за возбуждение Е-составляющей ЭМИ «отвечает» ток проводимости I₂, протекающий по металлическому цилиндру (конусу, плоской пластине) S₂ длиной l₂, тогда как H-составляющую ЭМИ создает ток смещения I₁ между кольцевым диском S₁, и подстилающей проводящей поверхностью S₀, удаленными друг от друга на расстояние l₁,

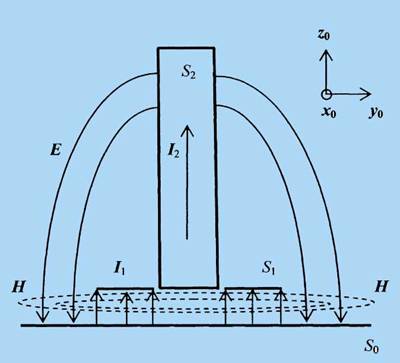
Рис. 3 Принцип действия МРА (несимметричный вариант) на примере CFA

Для возбуждения тока I₁, с требуемым фазовым сдвигом 90° относительно тока I₂ в схему МРА на рис. 3 (аналогично индуктивности L на рис. 2) вводится фазирующее устройство с делителем мощности сигнала, поступающего со сдвигом фаз 90° на диск S₁, и цилиндр S₂ (роль которых на рис. 2 выполняют развернутые пластины конденсатора). Симметрирование и согласование АФУ (устранение «антенного эффекта» и обеспечение заданного КСВ в фидерной линии) производятся обычным путем. Отметим, что критика описаний принципов действия CFA, SFRT-антенн и ЕH-антенн, которые содержат [3-9], не входит в задачу авторов настоящей статьи.

При электродинамическом моделировании МРА на рис. 3 будем исходить из того, что данную антенну можно представить в виде двух совмещенных элементарных электрических излучателей (ЭЭИ): длиной l₁ с током I₁, и длиной l₂ с током I₂, ориентированных в соответствии с единичным вектором l₀, причем l₂ > l₁ (оба ЭЭИ в составе МРА и вектор l₀ показаны на рис. 4 утолщенными линиями), в предположении, что размеры ее линейных элементов l_1,2 << λ. Азимутальный угол φ ; меридиональный угол Θ ; расстояние r от МРА до точки наблюдения М в сферической системе координат (совмещенной с декартовыми координатами, показанными на рис. 3); единичные векторы r₀ и φ₀ также обозначены на рис. 4.

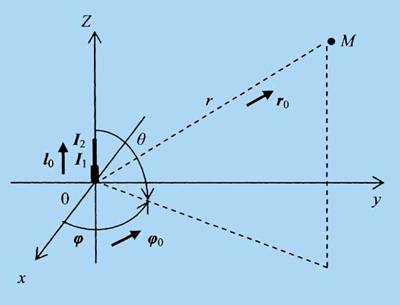
Рис. 4 К определению структуры ЭМИ в плоскости XOY для МРА

Воспользуемся записью решения уравнений Максвелла в обобщенном виде для двух совмещенных ЭЭИ [12-13], согласно которой

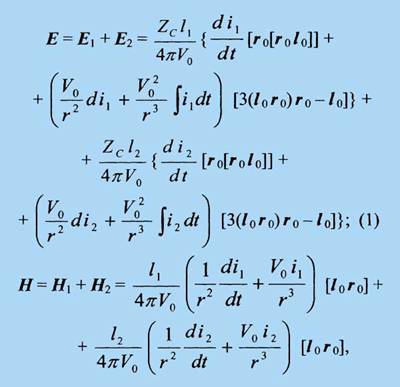
где Е и Н векторы напряженности, соответственно, электрического и магнитного поля (без нижних индексов - для МРА в целом; с индексами «1» для более короткого, с индексами «2» - для более длинного ЭЭИ); V₀ - скорость распространения радиоволн в окружающей среде; квадратные и круглые скобки обозначают, соответственно, векторные и скалярное произведения указанных на рис. 3-4 единичных векторов.

Без ущерба для общности результатов ограничимся анализом структуры поля МРА в плоскости XOY. Тогда при l₀ = z₀ получим      [l₀  z₀] = φ₀ , [r₀[r₀ l₀]] = – z_{0 ;}  3(l₀ r₀) r₀ – l₀  = – z₀ ; после чего (1) принимает вид

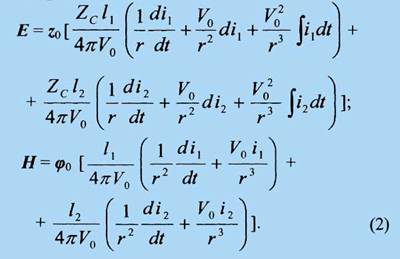
Чтобы учесть специфику возбуждения МРА данной конструкции (сдвиг по фазе на 90° токов, возбуждающих ЭЭИ), перейдем к комплексным амплитудам напряженностей поля (2) в скалярной форме [14]. Так как комплексные амплитуды токов, возбуждающих ЭЭИ, при этом будут равны I_m для I₁ и jI_m для I₂; а также с учетом dI₁/d_t = jωI_m ; dI₂/d_t = – ωI_m ;                                                                          

в итоге получим                              

        

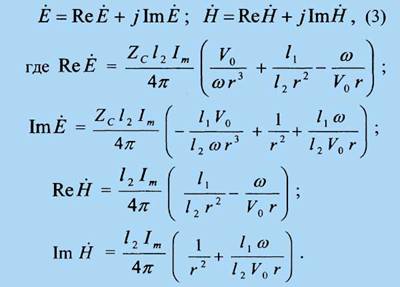
Анализ (3) показывает; во-первых, что уже на самых малых расстояниях от антенны: при r/λ << 1 и с учетом l₂ > l₁ структуру поля МРА действительно можно считать сформированной, поскольку здесь

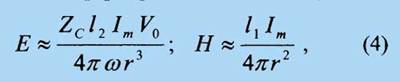
и волновой процесс уже связан с переносом энергии, так как вектор Пойнтинга для (4) есть действительная величина, при этом

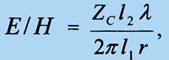
где Z_c волновое сопротивление окружающей среды.
Во-вторых, в зоне Фраунгофера: при r/λ >> 1 МРА ведет себя как обычный вибраторный излучатель, так как

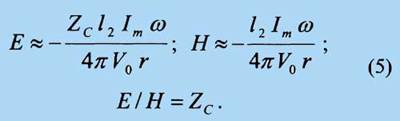
В-третьих, что при l₂ > l₁ согласно (3) уменьшается объем пространства вокруг антенны, в пределах которого сосредоточено реактивное поле - данное обстоятельство может иметь практическое значение, например, при использовании МРА в качестве эталонных излучателей и приемных измерительных антенн.
Каких-либо электродинамических «сюрпризов» конструкция МРА, по-видимому, не таит: решение системы уравнений Максвелла для ЭЭИ как в более общем временном виде [12-13], так и в рамках метода комплексных амплитуд для гармонического сигнала [14] «работает» здесь ничуть не хуже, чем для антенн других типов [1-2].

Сопротивление излучения и добротность МРА

Модель (1)-(5) и рис. 3-4 не является единственно возможной при описании свойств МРА. Для уяснения принципа действия и определения основных параметров С-антенны (см. схему возбуждения на рис. 2) воспользуемся моделью в виде контура II вида [15], показанной на рис. 5.
К точкам возбуждения антенны А-А на рис. 2 и рис. 5 через коаксиальный фидер с волновым сопротивлением W_ф подключен генератор с внутренним сопротивлением R_г; реактивные элементы L=L₁+L₂ и С входят в состав контура II вида с сопротивлением активных потерь R, которое состоит из тепловых потерь r в проводниках L и диэлектрике С, а также (в подавляющей мере) сопротивления излучения R_Σ МРА.

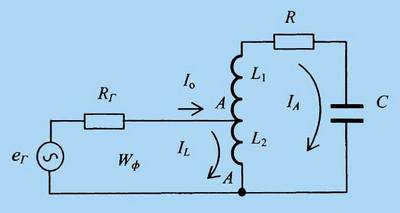
Рис. 5 Эквивалентная схема С-антенны в виде контура II вида с потерями.

Частичное подключение индуктивности p=L₂ /L обеспечивает согласование С-антенны, критерием которого является значение КСВ

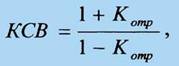
где К_отр - модуль коэффициента отражения по напряжению (току) от конца фидерной линии в точках А-А. Теоретический анализ МРА разделим на две части: решение задачи о широкополосном согласовании генератора с антенной (с учетом резонансных свойств МРА) и исследование частотной зависимости уровней ЭМИ, создаваемых МРА в окружающем пространстве. При решении первой задачи с использованием схемы на рис. 5 будем исходить из того, что имеет место согласование фидера по входу (R_г=W_ф). Тогда условие максимальной «нагрузки» генератора на МРА (максимальное согласование МРА с фидерной линией) требует R_AA=W_ф, критерием чего является экспериментально подтверждаемое условие КСВ = 1 [1-2].
Для упрощения выкладок введем на рис. 5 следующие обозначения:

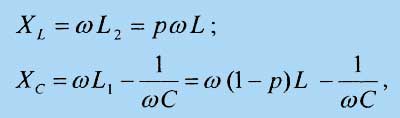
после чего выражение для комплексного входного сопротивления МРА в точках А-А приобретает вид

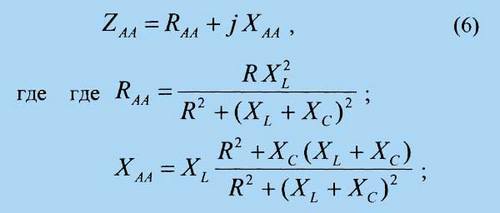
R - сопротивление активных потерь. Проанализируем резонансные свойства МРА. Условием параллельного резонанса на частоте

в контуре II вида является X_L + Х_C = О, откуда согласно (6) получаем

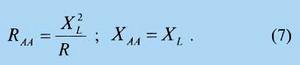
Аналогичным образом, условием последовательного резонанса на частоте

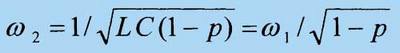
в контуре II вида является X_с=0, откуда следует

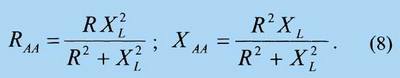
Условиям максимального согласования МРА с фидером на неизвестной частоте ω_о, согласно (6), соответствуют равенства

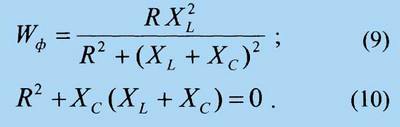
Распишем знаменатель (9) как

и используем (10) после чего на частоте ω_о, получим (9) в следующем виде

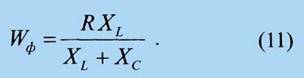
Выразим из (11) сопротивление потерь R и после подстановки его в (10) получим уравнение, в котором единственным неизвестным будет частота ω_о :

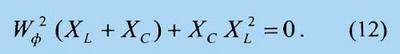
Из (12) получим для ω_о биквадратное уравнение

   

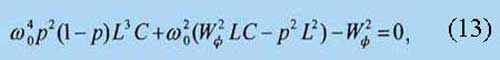
решение которого имеет вид

  

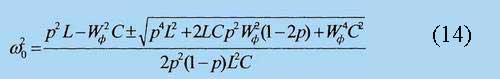
В случае 2p << 1 (при достаточно малом частичном подключении фидера к С-антенне) из (14) следует,

то есть частота максимального согласования совпадает с частотой последовательного резонанса. Полученный результат позволяет интерпретировать «физический смысл» сопротивления R следующим образом. Поскольку на частоте со значение КСВ = 1; Х_AA = 0 и R_AA  = W_ф ; С-антенна для фидерной линии представляет собой согласованную нагрузку, коэффициент отражения К_отр = 0 и вся активная мощность, развиваемая генератором, делится поровну между его внутренним сопротивлением R_г и сопротивлением R, величина которого учитывает потери в контуре II вида. Если считать, что r << R_Σ, приходим к выводу, что в данном случае, во-первых, R ≈ R_Σ = W_ф , а во-вторых, КПД у С-антенны η ≈ 1 . Полученные результаты говорят о том, что теория электрически короткого диполя неприменима к работе С-антенны при резонансе, так как R_Σ для d << λ здесь, по классическим представлениям, не должно превышать 1 Ом [1], тогда как W_ф = 50-75 Ом.
Добротность частично подключенного к фидерной линии контура II вида с потерями определяется как Q = W_k /(R+pW_ф), где

- его характеристическое сопротивление [15].

Поскольку ширина полосы пропускания есть

для МРА здесь имеет место

Таким образом, коэффициент p=L₂ /L является одним из возможных параметров регулировки широкополосности МРА - наряду с величиной отношения C/L, в котором для увеличения относительной полосы

целесообразно увеличивать емкость С-антенны - тем более, что для сохранения резонансной частоты

в данном случае требуется уменьшение индуктивности L (если все это возможно по конструктивным причинам [1; 16]). Анализ показывает, что для типовых значений L; C; Ρ и W_ф ожидаемые значения добротности МРА Q ≈ 5...15, что соответствует

Частотная зависимость мощности излучения МРА

Для исследования структуры уровней ЭМИ, создаваемых МРА в окружающем пространстве, необходимо проанализировать частотные свойства сопротивления излучения R_Σ = R и активной мощности излучения P_A = 1/2 I²_A R_Σ  - если считать, что последующий расчет уровней Е- и Н-составляющих ЭМИ не представляет труда. Комплексное напряжение на входе МРА, в соответствии с обозначениями на рис. 5 и в (6), будет равно

где ток İ_L = İ₀ – İ_A . Из (15) получаем

 

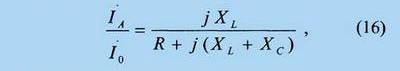
и после перехода к амплитудам токов

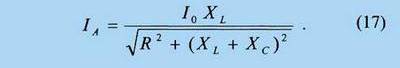
Отсюда следует, что при параллельном резонансе на частоте ω₁ имеет место I_A = I₀ X_L /R, а при последовательном резонансе на частоте ω₂ ток

где оценку соотношения между токами осложняет неизвестная частотная зависимость R. Общее выражение для излученной мощности при этом имеет вид:

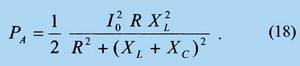
При максимальном согласовании МРА на частоте ω₀ ≈ ω₂ излученная мощность

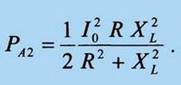
Частотные свойства Р_А будем исследовать путем анализа отношения

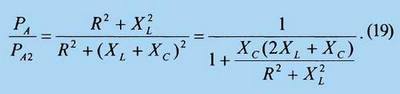
При последовательном резонансе (X_C=0) здесь Р_А = Р_А2, и вопрос теперь в том, существует ли область частот ω₃, в которой отношение Р_А /Р_А2 достигает максимума, и где на оси частот располагается эта область. Из анализа (19) вытекают следующие необходимые условия выполнения Р_A >Р_A2 :

которым соответствует условие

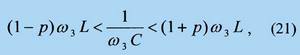
приводящее к двухстороннему неравенству

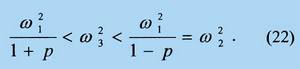
Отсюда следует, что область частот ω₃ во-первых, существует, а во-вторых, располагается на оси частот ниже ω₁ и ω₂. Поэтому максимум согласования МРА с фидерной линией (на частоте ω₀) не совпадает с максимумом излученной мощности (на частоте ω₃), хотя при ожидаемых значениях добротности МРА Q это несовпадение может не иметь практического значения. Тем не менее, настройка С-антенны по максимальному согласованию (КСВ = 1 на частоте ω₀) не соответствует условию обеспечения максимума уровней ЭМИ в окружающей среде - о чем специалистам, занятым проектированием и эксплуатацией С-антенн [10-11], известно достаточно хорошо.

Результаты экспериментально-аналитических исследований.

Для дальнейшего исследования МРА воспользуемся экспериментально-аналитическим методом, который сочетает использование результатов расчетов и непосредственных измерений, выполненных на макете (физической модели) МРА. Макет плоской С-антенны из фольгированного стеклотекстолита с размерами 85 х 15 мм был рассчитан на среднюю частоту рабочего диапазона 100 МГц. Для сравнительных измерений также был  изготовлен  полуволновой  диполь (далее  λ/2-диполь) с габаритным  размером 2l = 1,46 м. Определение параметров АФУ производилось с помощью лабораторной установки, показанной на рис. 6.

В качестве генератора сигнала и измерителя КСВ на рис. 6 использовался прибор РК2-47; в качестве детектора поля излучения - измерительная антенна АИ5-0, подключенная к анализатору спектра  R&S  FS-300. Антенны в помещении лаборатории располагались на высоте 1,22 м от пола и на расстоянии 3 м друг от друга. Для симметрирования фидера, подключенного к С-антенне, применялся ВЧ фильтр-пробка на ферритовом кольце (см. рис. 6), эффективность которого проверялась путем контроля «антенного эффекта» коаксиального кабеля.

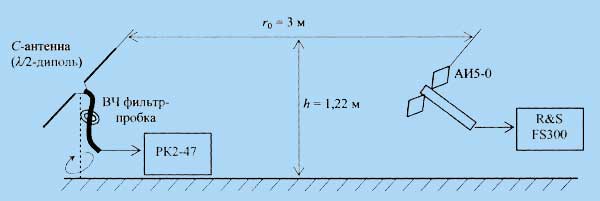
Рис. 6 Схема лабораторной установки для исследования С-антенны и λ/2-диполя.

Согласно [3; 16]  для макета МРА с центральной частотой рабочего  диапазона ƒ = 100 МГц  значения С = 1,25 пФ; L = 2,0 мкГн. После учета собственной емкости катушки индуктивности (длина 22,5 мм; диаметр витка 17 мм; число витков 11,6) емкость С ≈ 2,95 пФ, что дает L ≈ 0,9 мкГн с соответствующим уменьшением числа витков.

В таблице 1 (двойная первая строка и вторая строка) представлены результаты измерения КСВ ≤ 2,3 в полосе частот ƒ = 93-100,4 МГц для рассматриваемого макета плоской С-антенны с параметрами: емкость С = 3 пФ; индуктивность L = 1 мкГн; коэффициент р = 0,5; частота параллельного резонанса ƒ₁ = 68,6 МГц; частота последовательного резонанса ƒ₂ ≈ ƒ₀ = 97 МГц (совпадает с частотой максимального согласования АФУ), полученные с помощью установки, показанной на рис. 6. Отметим, что ожидаемое значение частоты максимума излученной мощности ƒ₃ ≈ 60 МГц находится за пределами области частот ƒ, в пределах которой, по данным таблицы 1, значения КСВ ≤ 2,3. Минимальный КСВ на частоте 97 МГц для С-антенны и 102 МГц для λ/2-диполя равняется 1,3; ширина полосы частот по уровню КСВ = 2 для  С-антенны - 7 МГц; для λ/2-диполя - 9 МГц.

Целью первого этапа конструирования С-антенны является выбор приемлемой конфигурации пластин конденсатора, при которой может быть реализована контурная катушка индуктивности на заданную резонансную частоту. На втором этапе при настройке МРА методом последовательных приближений добиваются необходимых резонансов и полос излучения АФУ: изменяя либо С, либо L и место отвода (значение коэффициента p) в С-антенне. Практические методики настройки  МРА  приводятся  в  [3-4; 10-11].

Соответствующие измеренным КСВ экспериментальные значения коэффициента отражения К_отр от нагрузки (входа С-антенны в точках А-А) по напряжению (току), соответствующие теоретической формуле

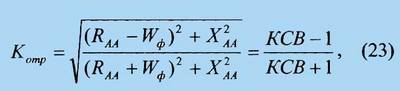
приведены в третьей (первой снизу) строке таблицы 1.

На основании (23) с учетом (6) можно построить итерационную процедуру определения сопротивления излучения R_Σ = R на каждой из частот, приведенных в таблице 1, которая предусматривает следующие действия.

Задавая на каждой частоте первоначальное значение

где К_отр соответствует данным таблицы 1, производим расчет R_AA и X_АА согласно (6), подставляем их в (23) и получаем расчетные значения К_отр и КСВ, которые сравниваем с их табличными значениями и, в случае расхождения между ними, изменяем величину R, после чего повторяем цикл до тех пор, пока расчетные и экспериментальные значения К_отр и КСВ будут отличаться друг от друга не более чем на заданную величину ε << 1 . Найденное  таким  образом значение  R = R_Σ  считаем  сопротивлением  излучения     С-антенны на данной частоте. Практика показала, что после 2-3 компьютерных итераций с использованием пакета Mathcad в диалоговом режиме, во-первых, удается получить ε < 0,1 для КСВ,  а во-вторых, что значение R_Σ , найденное на частоте ƒ₀ = 97 МГц, в полосе частот ƒ = 93-100,4 МГц изменяется достаточно мало.

Таблица № 1 Частотные зависимости КСВ; К_отр и R_Σ для макета С-антенны (ƒ₀ = 97 МГц)

 

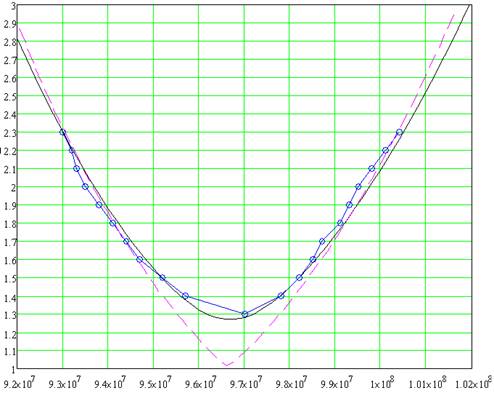
Рис. 7 Рсчетные и экспериментальные значения КСВ для макета С-антенны.

На рис. 7 экспериментальные значения КСВ показаны точками; график в виде сплошной линии соответствует расчету с помощью (23) при R_Σ = 63 Ом; С = 2,75 пФ; L = 1,96 мкГн график в виде штриховой линии - расчету при R_Σ = W_ф = 50 Ом; С = 2,9 пФ; L = 1,86 мкГн. Сравнение между собой данных на рис. 7 показывает, во-первых, что степень различия между ними не превышает общей (методической и инструментальной) погрешности измерений, проводимых на макете С-антенны в лабораторных условиях. Во-вторых, что путем корректировки параметров МРА R_Σ и С в достаточно малых пределах с помощью итерационной процедуры (23) можно достаточно точно описать экспериментальную зависимость КСВ реальной С-антенны от частоты.
Эффективность АФУ оценивалась методом сравнения уровней напряженности поля, создаваемых в заданном направлении С-антенной и λ/2-диполем на расстоянии r₀ ≈ λ в E-плоскости. Сравнительные спектрограммы сигналов на выходе АФУ приведены на рис. 8 (верхние графики на рис. 8а - С-антенна; на рис. 8б - λ/2-диполь; нижние графики - электромагнитный фон в помещении лаборатории при выключенных приборах).

Левая маркерная линия на рис. 8а соответствует нижней границе полосы частот по уровню КСВ = 2; правая маркерная линия - центральной частоте настройки С-антенны по КСВ. Вертикальный маркер на рис. 86 установлен на центральной частоте согласования λ/2-диполя по КСВ.
Из анализа данных рис. 8 видно, что оба АФУ создают в точке приема соизмеримые уровни Е; дБ, однако С-антенна обладает заметно меньшим (на 10-15 дБ) уровнем побочного излучения (см. полосу частот 50-80 МГц справа от маркеров на рис. 8а), что объясняется существенно меньшим числом побочных гармоник и других резонансных частот у С-антенны по сравнению с λ/2-диполем.

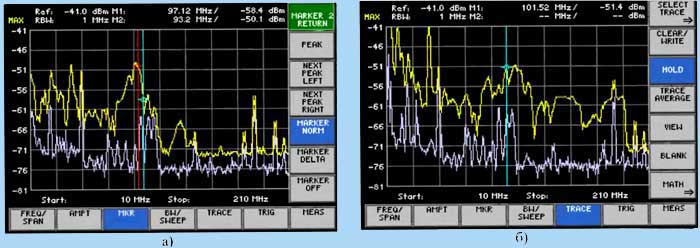
Рис. 8 Спектры излучения АФУ на расстоянии 3м: а) С-антенна; б) λ/2-диполь.

Максимальные уровни напряженности поля Е; дБ, от сравниваемых антенн при разных фиксированных значениях азимутального угла φ, град в E-плоскости представлены в таблице 2. Из таблицы 2 видно, что различие уровней Е у данных АФУ составляет от -3,1 до 1,3 дБ, что свидетельствует о сравнительной эффективности С-антенны (укороченная до таких же размеров стандартная антенна на 10 дБ и более уступала λ/2-диполю[1-2]).
Экспериментальная диаграмма направленности С-антенны в E-плоскости с погрешностью ±1 дБ является изотропной, что соответствует ее определению как МРА.

Таблица № 2 Уровни напряженности поля для С-антенны и λ/2-диполя при фиксированных азимутальных углах φ, град в E-плоскости.

 

На рис. 9 представлены результаты расчета частотных зависимостей для отношения Р_А / P_A2 согласно (19) - левые кривые с экстремумами в виде максимума, значения отложены на левой вертикальной оси; и КСВ согласно (23) - правые кривые с экстремумами в виде минимума, значения отложены на правой вертикальной оси. Графики рис. 9а соответствуют коэффициенту подключения р = 0,5 и наглядно иллюстрируют  несовпадение  условий  максимального  согласования  и  максимального  излучения С-антенны, устранение которого представляется принципиальной проблемой МРА. Графики рис. 96 демонстрируют возможный способ решения данной проблемы, связанный с уменьшением р. Напомним, что авторы [10-11] с данной особенностью настройки МРА знакомы достаточно хорошо.

 

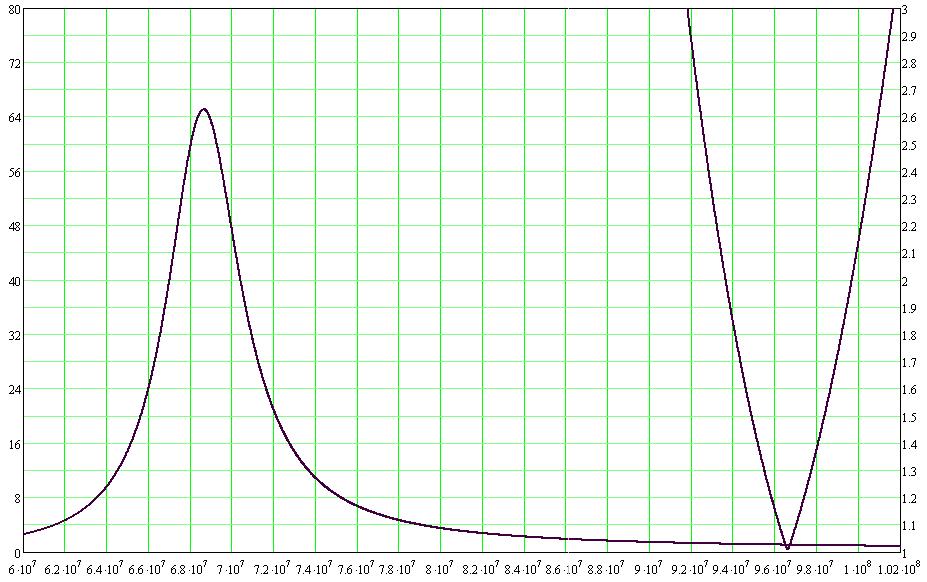
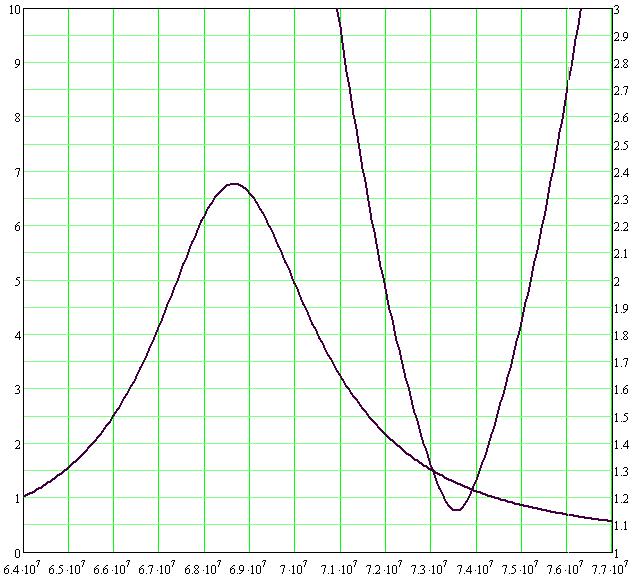
а)                                                                                                                              б)

 

Рис. 9 Совмещенные расчетные графики частотных зависимостей Р_А /P_A2 (левые кривые) и КСВ (правые кривые) для макета С-антенныа при р = 0,5; б) при р = 0, 15

Выводы

Результаты экспериментов и опытной эксплуатации новых типов МРА показывают как многообещающие свойства данных АФУ (малые размеры, повышенные широкополосность и помехозащищенность, малочувствительность к посторонним Е- и H-полям и т.д.), так и сложности, связанные с их проектированием, настройкой и практической эксплуатацией. Изложенные методики и результаты комплексного  (аналитического и экспериментального)  исследования  МРА  в  виде  макета  плоской С-антенны не выходят за рамки традиционной теории АФУ [1-2], но демонстрируют специфические особенности МРА, к которым могут быть отнесены:

• возможность значительного увеличения сопротивления излучения по сравнению с другими малогабаритными АФУ;
• существенное влияние резонансных явлений на рабочие характеристики МРА;
• существенное уменьшение объема пространства вокруг АФУ, в пределах которого сосредоточено реактивное поле;
• возможность регулировки широкополосности и добротности МРА путем изменения коэффициента подключения р;
• различие условий максимального согласования МРА с питающим фидером (по минимуму КСВ) и максимального излучения МРА (по максимуму отношения Р_А /P_A2 );
• существенное влияние паразитных реактивностей и фактора нестабильности параметров на режим работы и характеристики МРА.

Наряду с продолжением комплексных исследований и совершенствованием методов анализа и проектирования МРА представляет интерес применение статистической теории антенн для статистического имитационного моделирования МРА.

Литература

1.     Айзенберг ГЗ. Коротковолновые антенны. М.: Связьиздат, 1962. - 816 с.

2.     Надененко С.И. Антенны. М.: Связьиздат, 1959.-552 с.

3.     http://eh-antenna.com

4.     http://eh-antenna.net

5.     http://dtirfswolutions.com

6.     http://crossedfieldantenna.com

7.     EH Antenna (EH antenna). US Patent 6,486,846. Robert T. Hart, Nov. 26, 2002. Appl. No.: 09/576,449. Field: May 23, 2000.

8.     Method and Apparatus for Creating an EH Antenna (Метод и аппарат для создания ЕН антенны). Robert T. Hart, June 12, 2003. serial No.:302952~Series Code: 10. Field: Nov. 22, 2002. US Current Class: 346/860; 343/773; 343/870 US Class at Publication: 346/860; 343/773; 343/870. Intern. Class: H01Q001/50; H01Q0123/00 Discription

9.     Radio Antennas (Радио антенна) US Patent No.: 5,155,495 Maurice C. Hately, Fathi M. Kabbary, October 13, 1992. Appl. No.:543,768. Filed: Jan 27, 1989.

10. http://www.ehant.narod.ru

11. http://flateh.narod.ru

12. Хармут Х.Ф. Теория секвентного анализа: основы и применение. Пер. с англ. М.: Мир,1980.-575 с.

13. Маслов О.Н. Устойчивые распределения и их применение в радиотехнике. М.: Радио и связь, 1994.-152 с.

14. Н.Вольман В.И., Пименов Ю.В. Техническая электродинамика. М.: Связь, 1971. 487с.

15. 3ернов Н.В., Карпов В.Г Теория радиотехни-ческих цепей. Л.: Энергия, 1972. - 816 с.

16. Иоссель Ю.Я., Кочанов Э.С., Струнский М.Г. Расчет электрической емкости. Л.: 1969. - 240 с.

Маслов Олег Николаевич, д.т.н., профессор Кафедры «Экономические информационные системы» Поволжского государственного университета телекоммуникаций и информатики (ПГУТИ). Е-mail: maslov@psati.ru
Рябушкин Аркадий Викторович, инженер Кафедры «Мультисервисные системы и безопасность» ПГУТИ. Е-mail: ryabushkin@psati.ru
Шашенков Валерий Федорович, к.т.н., с.н.с., соискатель ПГУТИ. Е-mail: maslov@psati.ru

Подписной индекс 46832 в каталоге ОАО Агентства «Роспечать».

Статью в формате PDF можно скачать ЗДЕСЬ

| главная | | W5QJR| | UA1ACO | | Теория | | Практика | | Россия | | Германия | | Украина | | США | | Швеция | | Швейцария| | Италия | | Австралия | | Франция | | Серийные | | Ссылки | | Разное |